23rd August 2018 3:06 am
Programming Challenges (part 1 - Knuth Arrow)

On my github I’ve started sporadically doing programming challenges in my spare time. Since Python is the easiest language for me to put down and pick back up I’ve opted for doing these in that language, though I might see about returning to some of these in other languages.
These programming challenges come from a phone app linked up to r/dailyprogrammer. Today I’m looking at a Beginner Challenge, Knuth’s Arrow, just for simplicity.
(BEGINNER) Knuth’s Arrow:
For a lot of these programming challenges the hardest part is often trying to figure out just what the concept behind the challenge is. From Wikipedia:
In mathematics, Knuth’s up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976.
Essentially, Knuth arrow is iterated exponentiation, the same way exponentiation is basically just iterated multiplication and multiplication is iterated addition. So one 2↑2 is the same as 2^2, since there’s only one arrow.
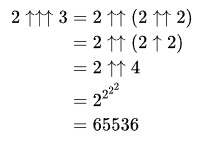
Thankfully, the reason this problem is ‘beginner’ is because Knuth Arrow follows a pretty simple formula that just needs to be replicated in code:
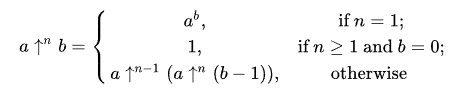
So, this is exactly as Wikipedia says:
“…more than one arrow means iterating the operation associated with one less arrow.”
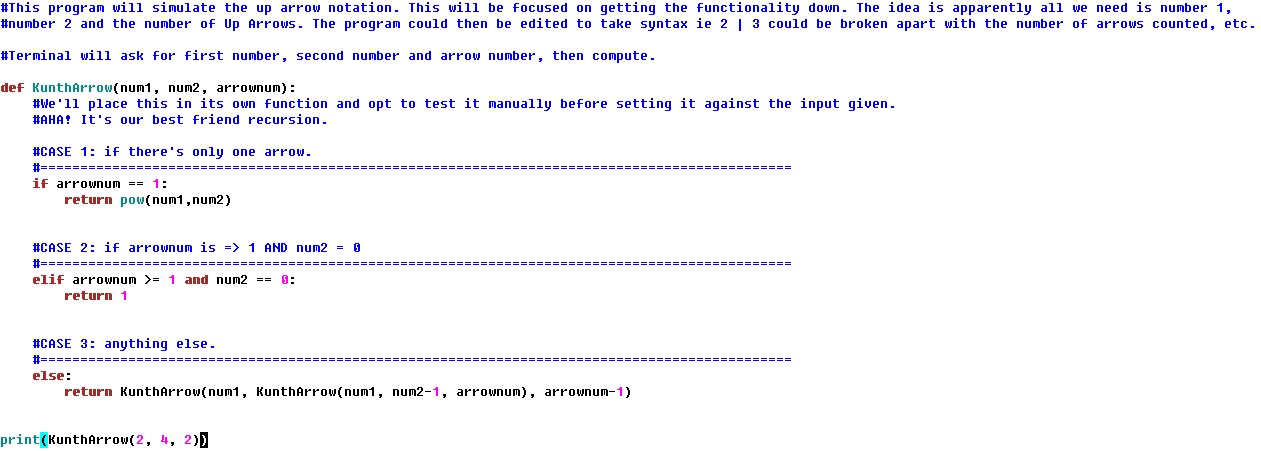
Right away this can be seen as a recursion problem. It’s just compounding knuth arrow formulas on top of one another until you reach one of two terminating cases. Thus, the program is fairly short:
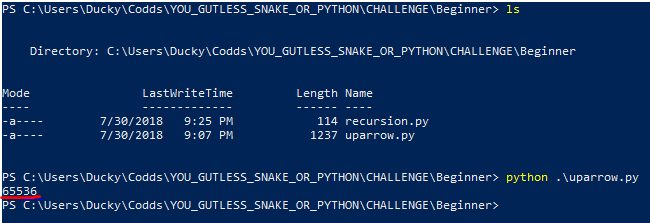
For the sake of simplicity, it just runs with test values. Here shown it’s given test values 2↑↑4. This is expected to produce 2↑(2↑(2↑2)) or 65536. Checking our output we see that the program outputs exactly that:
Some of the challenge input include 5↑↑↑↑5 and 7↑↑↑↑↑3. This is an excellent way to test the output. Problem is, when I ran with these inputs (ie 5,5,4) the program would seemingly hang. A couple of print statements showed the problem. Or rather the lack of a problem. When they say the Knuth arrow is used to denote massive numbers they’re not kidding. 5↑↑↑↑5 has intermediate numbers that fill up multiple screens with digits you have to scroll through. It’s likely integers on my computer aren’t equipped to simply print out numbers from a Knuth arrow. Thus, later I’ll need to do a rewrite that simple strings a string for the full knuth arrow equation with no computation.
Right now on my programming challenges Repo I have unfinished code for creating Ducci sequences, so finishing that up will be my next goal when I can find the time.
~Nicko
